
◇知识详解
知识点1:排列组合
在现实生活中我们经常会遇到排座次、分配任务等问题,用到的都是排列组合原理,即便是最简单的概率问题也要利用排列组合原理计算。与此同时,排列组合中还有很多经典问题模型,其结论可以帮助我们速解该部分题型。
1.基本原理
加法原理:m1+m2+……+mn
乘法原理:m1×m2×……×mn
小结:分类用加法原理,分步用乘法原理
2.计算方式
排列:![]()
组合:![]()
小结:考虑顺序用排列,不考虑顺序用组合。
3.基本解题策略
3.1合理分类策略
①类与类之间必须互斥(互不相容);②分类涵盖所有情况。
3.2准确分步策略
①步与步之间互相独立(不相互影响);②步与步之间保持连续性。
3.3先组后排策略
当排列问题和组合问题相混合时,应该先通过组合问题将需要排列的元素选择出来,然后再进行排列。
例题1.奶奶有6 颗口味各不相同的糖,现分给3 个孙子,其中1 人得1 颗、1 人得2 颗、1人得3颗,则共有( )种分法。
A.60 B.120 C.240 D.360
【志远快解】:此题答案为D。此题既涉及排列问题(参加6颗口味各不同的糖),又涉及组合问题(分给三个孙子,每人分得糖数不同),应该先组后排。先按颗数分堆,1颗有![]() 中情况,接下来2颗有
中情况,接下来2颗有![]() 种可能,剩下的就是3颗的。故分堆有6×10=60种情况。对任一情况,没人分一堆,相当于把3堆全排列,有
种可能,剩下的就是3颗的。故分堆有6×10=60种情况。对任一情况,没人分一堆,相当于把3堆全排列,有![]() =6种情况,共有60×6=360种分法。
=6种情况,共有60×6=360种分法。
4.排列组合问题特殊解法
排列组合问题用到的方法比较特殊,缘于这些方法都是在对问题进行变形,把不容易理解的问题转化为简单的排列组合问题。
4.1捆绑法
排列时如要求几个元素相邻,则将它们捆绑起来视为一个整体参与排列,然后再考虑它们内部的排列情况。
例题2.某展览馆计划4月上旬接待5个单位来参观,其中2个单位人较多,分别连续参观3天和2天,其他单位只参观1天,且每天最多只接待1个单位。问:参观的时间安排共( )种。
A.30 B.120 C.2520 D.30240
【志远快解】:答案C。4月上旬有10天。在这10天里接待5个单位,其中两个单位分别“连续参观”3天和“连续参观”2天。则将连续的3天捆绑为1份,连续的2天捆绑为1份。现在仍有10-2-3=5天,即余下的5天为5份,那么10天共可分为7份。在这7份中选5份接待5个单位,即有![]() 种。
种。
排列时如要求几个元素不相邻,则把不能相邻的元素插到其他元素形成的“空隙”中去。
例题3.将三盆同样的红花和四盆同样的黄花摆放成一排,要求三盆红花互不相邻,共有多少种不同的方法?( )
A.8 B.10 C.15 D.20
【志远快解】:答案B。四盆黄花两侧可形成5个空隙,要使三盆红花互不相邻只需从中选取3个空隙放入红花即可,![]() =10。
=10。
4.3插板法
若要求把n个元素分成m堆(每堆至少有1个),则把(m-1)个木板插入这n个元素形成的(n-1)个“空隙”中去可实现上述要求,计算方式![]() 。
。
例题4.某单位订阅了30份学习材料发放给3个部门,每个部门至少发放9份材料。问一共有多少种不同的发放方法?( )
A.7 B.9 C.10 D.12
【志远快解】:答案C。先给每个部门发8份,8×3=24,还剩下30-24=6份,将6份发给3个部门,每个部门至少分一个,就能保证每个部门至少分9份,列式为![]() =10。
=10。
4.4分析问题对立面
很多问题分类讨论起来很麻烦,但是它的对立面却很好计算,此时只需要算出总体的情况数再减去对立面的情况数。
例题5.某班同学要订A、B、C、D四种学习报,每人至少订一种,最多订四种,那么每个同学有多少种不同的订报方式?( )
A.7种 B.12种 C.15种 D.21种
【志远快解】:答案C。“至少1种,至多4种”,结合题干,其反面是“1本都不订”。每种报纸有订或不订2种选择,则共有2×2×2×2=16种订法,反面情况为1种,则所求就是16-1=15种。
知识点2:概率问题
概率是一个介于0到1之间的数,是对随机事件发生可能性的测度。概率问题经常与排列组合结合考查。因此解决概率问题要先明确概率的定义,然后运用排列组合知识求解。
1.传统概率问题
将所有的情况分成n个等可能的情形,事件A包括了其中的m个情形,那么称事件A发生的概率![]() 。
。
假设事件B发生为“事件A没有发生”,则事件B的对立面为“事件A一定会发生”,即P(A)+P(B)=1,故P(A)=1-P(B)。
例题1.田忌与齐威王赛马并最终获胜被传为佳话。假设齐威王以上等马、中等马和下等马的固定顺序排阵,那么田忌随机将自己的三匹马排阵时,能够获得两场胜利的概率是( )。
![]()
![]()
![]()
![]()
【志远快解】:答案C。田忌必须以下等马对齐威王的上等马,以上等马对齐威王的中等马,以中等马对齐威王的下等马才能获胜两场,可供田忌选择的组合是![]() 种,所以他获胜的概率为1/6 。
种,所以他获胜的概率为1/6 。
[随堂练习一]
1.某小组有四位男性和两位女性,六人围成一圈跳集体舞,不同的排列方法有多少种?( )
A.720 B.60 C.480 D.120
2.一张节目表上原有3个节目,如果保持这3个节目的相对顺序不变,再添进去2个新节目,有多少种安排方法?( )
A.20 B.12 C.6 D.4
3.要求厨师从12种主料中挑选出2种、从13种配料中挑选出3种来烹饪某道菜肴,烹饪的方式共有7种,那么该厨师最多可以做出多少道不一样的菜肴?( )
A.131204 B.132132 C.130468 D.133456
4.盒中有4个白球6个红球,无放回地每次抽取1个,则第2次取到白球的概率是多少?( )
A.2/15 B.4/15 C.2/5 D.4/5
5.某射击运动员每次射击命中10环的概率是80%,5次射击有4次命中10环的概率是( )
A.80% B.63.22% C.40.96% D.32.81%
联系我们:
更多考试信息请关注:陕西志远教育官网(www.zyhtedu.org)
微信公众号:sxzyedu
QQ:623813217
志远教育,让您的起点与众不同!祝各位亲爱的考生圆梦2024!
| 西安校区:西安市雁塔区阳阳国际B座18楼 | 电话:029-87871887 17792273747(同微信) |
| 咸阳校区:咸阳市财富中心 | 电话:029-33275952 18142418653(同微信) |
| 延安校区:延安市东大街7天连锁酒店 | 电话:15353313055(同微信) |
| 渭南校区:渭南师范校内生活区 | 电话:18064315951(同微信) |
| 蒲城校区:迎宾路北段(火锅先生北邻) | 电话:18142418653(同微信) |
| 富平校区:莲湖大街中段(红莲酒店对面) |
电话:18142418353(同微信) |
| 铜川校区:铜川市宜君县南山公园 | 电话:15353313055(同微信) |
课程推荐: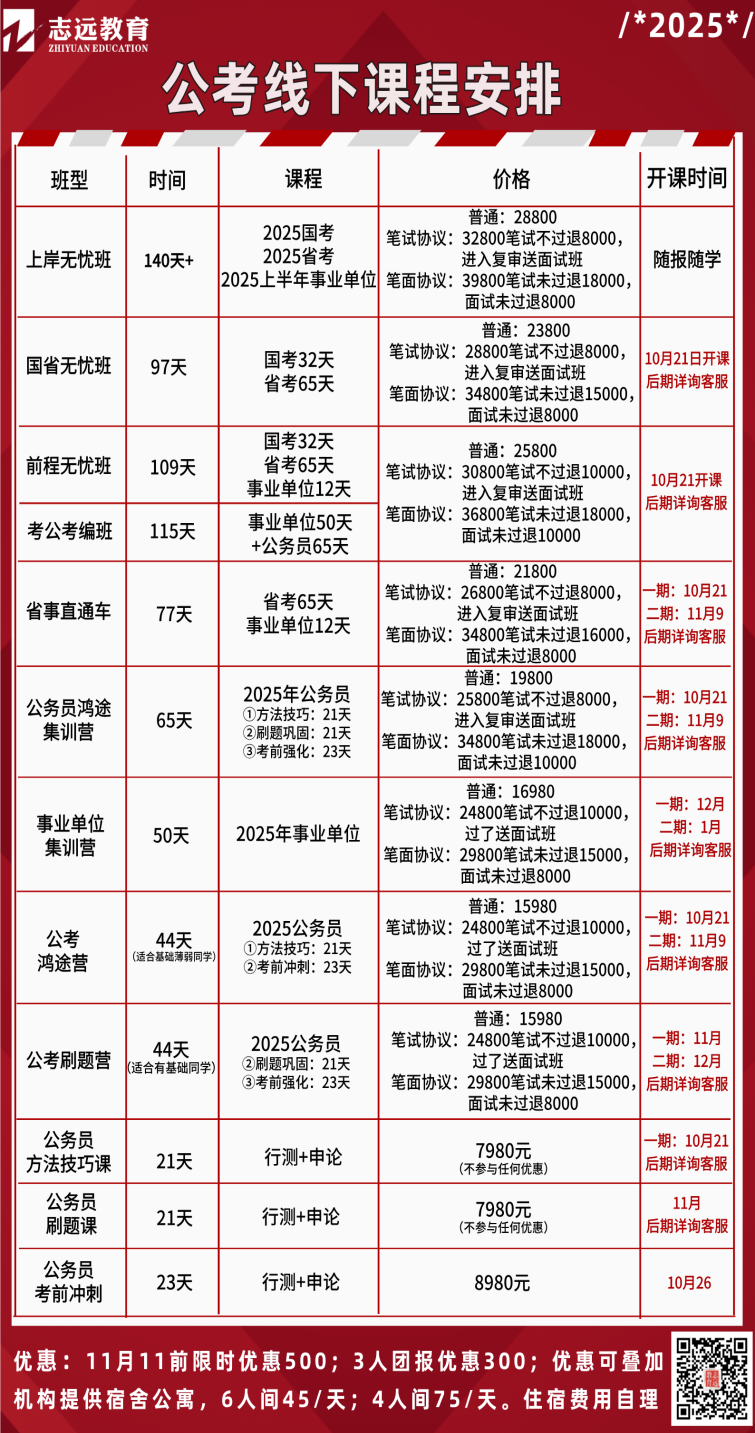


志远教育官网

微信二维码
微信号:17792273747Copyright © 陕西志远鸿途教育科技有限公司 版权所有
备案号:陕ICP备14003123号-1