
◇知识详解
知识点1:整数特性
1.常见小数字的整除判定
(1)局部看
一个数的末位能被2或5整除,这个数就能被2或5整除;一个数的末两位能被4或25整除,这个数就能被4或25整除;一个数的末三位能被8或125 整除,这个数就能被8或125 整除。
(2)整体看
整体作和:一个数各位数数字和能被3或9 整除,这个数就能被3或9整除;整体作差:如果一个整数的末三位与末三位以前的数字组成的数之差能被7、11 或13整除,那么这个数能被7、11或13整除。
截尾法:把个位数字截去,再从余下的数中,减去个位数的2倍,差是7 的倍数,则原数能被7整除。
(3)其他合数判断一个数能否被某个合数整除,一般的方法是先把这个合数分解成几个容易判断整除的数的乘积的形式,并且这些数两两互质,再分别判断。
2.整除思想的应用环境
(1)文字描述整除:明显整除字眼、出现“每”“平均”“倍数”等;
(2)数据体现整除:出现分数、百分数、比例、小数等。
例题1.一个两位数的中间加上一个0,那么所得的这个数是原数的9 倍,原来这个两位数是多少?( )
A.15 B.25 C.35 D.45
【志远快解】:答案D。解析:根据题意可知,原数各位数字之和能被9整除,观察选项只有D项符合。
例题2.已知甲、乙两人共有260本书,其中甲的书有13%是专业书,乙的书有12.5%是专业书,问甲有多少本非专业书?( )
A.75 B.87 C.174 D.67
【志远快解】:答案B。解析:由“甲的书有13%是专业书”可知,甲有87%的非专业书,由此可推出甲的非专业书是87的倍数,排除A、D,代入B满足题意。
例题3.一袋糖里装有奶糖和水果糖,其中奶糖的颗数占总颗数的60%。现在又装进10颗水果糖,这时奶糖的颗数与总颗数的比为4∶7,那么,这袋糖里有多少颗奶糖?( )
A.100 B.112 C.120 D.122
【志远快解】:答案C。解析:已知奶糖的颗数占总颗数的60%,即奶糖的颗数∶总颗数=3∶5,可知奶糖的颗数能被3整除,结合选项,只有C满足,故选C。
例题4.如果单独完成某项工作,那么甲需24 天,乙需36 天,丙需48 天。现在甲先做,乙后做,最后由丙完成。甲、乙工作的天数比为1∶2,乙、丙工作的天数为3∶5。则完成这项工作共用了多少天?( )
A.30 B.38 C.32 D.40
【志远快解】:答案B。解析:根据题意可得,甲乙丙工作天数之比为3∶6∶10,所以完成总工程需要 的时间是3+6+10=19 的倍数,结合选项,选择B。
例题5.甲乙丙丁四个人分6袋实物,他们的重量分别是12,16 ,20 ,24 ,28 ,36公斤,甲先取走一袋,剩下的由乙丙丁取走,已知乙和丙取走的重量一样多,且都是丁的2倍,每袋实物不能拆分,那么甲先取走的为多少?( )
A.16kg B.24kg C.28kg D.36kg
【志远快解】:答案D。解析:显然乙丙丁总和是5 的倍数,而12,16,20,24,28,36除以5 余2,1,0,4,3,1,即总重量除5余1,故甲也是除5余1,甲只能是D。
知识点2:和差倍比
1.主要的题型分为以下几类:
①和倍问题:已知两个或两个以上的数的和及它们之间的倍数关系,求这两个数或这些数各是多少?
例如:已知甲、乙两数之和是50,甲数是乙数的4倍,问甲、乙数分别是多少?
②差倍问题:已知两个数的差及其倍比关系,求这两个数各是多少。
例如:已知甲数是乙数的4倍,甲数比乙数多30,问甲、乙数分别是多少?
③比例问题:已知两个量之间的比例关系中和其中的一个量,求另一个量。比重也是比例问题中的一种情况。
例如:已知某班有50人,男生占总人数的40%,问这个班男生有多少人?
④连比关系:已知甲∶乙=a∶b,乙∶丙=c∶d,求甲∶乙∶丙。
例如:甲∶乙=3∶4,乙∶丙=3∶5,求甲∶乙∶丙。
2.解题方法
2.1公式法
和倍问题:和÷(倍数+1)=1倍量,1倍量×倍数=几倍量。
差倍问题:差÷(倍数-1)=1倍量,1倍量×倍数=几倍量。
比例问题:分量÷总量=所占比例,分量÷所占比例=总量。
注意事项:注意和差总数与倍数的对应关系,同时,要注意恰当选取单位“1”,使问题简化。
例题1.三个单位共有180人,甲、乙两个单位人数之和比丙单位多4倍,甲单位比乙单位多![]() ,则甲单位有多少人?( )
,则甲单位有多少人?( )
A.30 B.60 C.90 D.120
【志远快解】:先将甲乙看做一个整体,利用甲乙之和与丙之间的和倍关系可以求出甲乙之和,再根据甲乙之间的和倍关系求得甲单位的人数。根据和倍关系,丙单位有180÷(4+1+1)=30人,则甲、乙两个单位人数之和为180-30=150人。再根据和倍关系,乙单位有150÷(![]() +1+1)=60人,甲单位有150-60=90人。所以正确答案为C。
+1+1)=60人,甲单位有150-60=90人。所以正确答案为C。
2.2方程法
除使用公式外,根据倍比关系设未知数,列方程求解往往是最直接的方法。应用方程法时,要注意未知数应尽量少,且利于计算。例如,已知甲是乙的![]() ,则可设甲为8x,乙为5x,在运算过程中即可避免分数出现,以简化运算。
,则可设甲为8x,乙为5x,在运算过程中即可避免分数出现,以简化运算。
例题2.某校高中学生是初中学生的![]() ,高三和初三学生毕业后,留下的高中学生与初中学生人数之比为12∶17。已知高三、初三的毕业生都是520人,现在学校中共有学生多少人?( )
,高三和初三学生毕业后,留下的高中学生与初中学生人数之比为12∶17。已知高三、初三的毕业生都是520人,现在学校中共有学生多少人?( )
A.1044 B.1160 C.1305 D.1410
【志远快解】:设原来高中学生有5x人,初中学生有6x人,可列方程![]() ,解得x=200,故现在学校中共有学生200×(5+6)-520×2=1160人。
,解得x=200,故现在学校中共有学生200×(5+6)-520×2=1160人。
3.3整除特性法
①对和差倍比问题,尤其是遇到含分数、百分数和比例的问题,可以根据题目中的倍数关系,结合选项,利用整除特性代入排除。
②对连比问题:已知甲∶乙=a∶b,乙∶丙=c∶d,求甲∶乙∶丙,可先寻找中间量b、c的公倍数,转化得到甲∶乙=ac∶bc,乙∶丙=bc∶bd,进而甲∶乙∶丙=ac∶bc∶bd。
例题3.某高速公路对于过往车辆的收费标准:大客车30元,小客车15元,小轿车10元。某日通过该收费站的大客车与小客车数量之比为5∶6,小客车与小轿车数量之比为4∶11,收取小轿车的通行费比大客车多210元,则这天这三种车辆共通过的数量为( )。
A.330 B.355 C.385 D.450
【志远快解】:中间量6、4的最小公倍数为12,将5∶6与4∶11分别转化为10∶12与12∶33,则大客车∶小客车∶小轿车=10∶12∶33。以10辆大客车、12辆小客车、33辆小轿车为一组。每组中收取小轿车的通行费比大客车多10×33-30×10=30元,所以这天通过的三种车一共有210÷30=7组。共7×(10+12+33)=385辆。
4.题型精讲
4.1和差倍问题
这里面包括和倍问题和差倍问题两种,考生需要分清楚和、差、倍之间的关系。
例题4.甲、乙两桶油的质量相等。如果从甲取出24千克,给乙桶加入18千克,这时乙桶质量是甲桶的3倍。两桶油原来有多少千克?( )
A.30 B.45 C.35 D.42
【志远快解】:差倍问题。从甲取出24千克,给乙桶加入18千克后,两桶油质量相差24+18=42千克,刚好对应乙比甲多出的3-1=2倍。则甲桶取出24千克后的质量为42÷(3-1)=21千克,所以甲、乙原来的质量为21+24=45千克。
4.2比例问题
比例问题一般涉及的是两个量之间的关系,可以利用方程法来做。
例题5.甲乙丙三个蔬菜基地共存放了5200吨蔬菜,如果从甲基地运出544吨放到乙基地后,乙基地的蔬菜比丙基地多800吨,且此时甲乙基地的蔬菜重量比为7∶4,则甲基地原有蔬菜的吨数为( )。
A.2256 B.2800 C.3059 D.3344
【志远快解】:设现在乙基地有蔬菜4x吨,那么现在甲基地有7x吨,丙基地有(5200-11x)吨,且现在乙基地的蔬菜比丙基地多800吨,则有4x-(5200-11x)=800,解得x=400,那么原来甲基地有蔬菜7×400+544=3344吨。
4.3连比问题
连比问题利用整除特性法,将两个数之间的关系转化成为三个数之间的统一关系。
例题6.三种动物赛跑,已知狐狸的速度是兔子的![]() ,兔子的速度是松鼠的2倍,一分钟松鼠比狐狸少跑14米,那么半分钟兔子比狐狸多跑多少米?( )
,兔子的速度是松鼠的2倍,一分钟松鼠比狐狸少跑14米,那么半分钟兔子比狐狸多跑多少米?( )
A.28 B.14 C.19 D.7
【志远快解】:由题意可知,三种动物的速度比为狐狸∶兔子∶松鼠=![]() ∶1∶
∶1∶![]() =4∶6∶3。一分钟松鼠比狐狸少跑14米,则兔子每分钟跑14÷(4-3)×6=84米,半分钟兔子比狐狸多跑84×(1-
=4∶6∶3。一分钟松鼠比狐狸少跑14米,则兔子每分钟跑14÷(4-3)×6=84米,半分钟兔子比狐狸多跑84×(1-![]() )÷2=14米。
)÷2=14米。
联系我们:
更多考试信息请关注:陕西志远教育官网(www.zyhtedu.org)
微信公众号:sxzyedu
QQ:623813217
志远教育,让您的起点与众不同!祝各位亲爱的考生圆梦2024!
| 西安校区:西安市雁塔区阳阳国际B座18楼 | 电话:029-87871887 17792273747(同微信) |
| 咸阳校区:咸阳市财富中心 | 电话:029-33275952 18142418653(同微信) |
| 延安校区:延安市东大街7天连锁酒店 | 电话:15353313055(同微信) |
| 渭南校区:渭南师范校内生活区 | 电话:18064315951(同微信) |
| 蒲城校区:迎宾路北段(火锅先生北邻) | 电话:18142418653(同微信) |
| 富平校区:莲湖大街中段(红莲酒店对面) |
电话:18142418353(同微信) |
| 铜川校区:铜川市宜君县南山公园 | 电话:15353313055(同微信) |
课程推荐: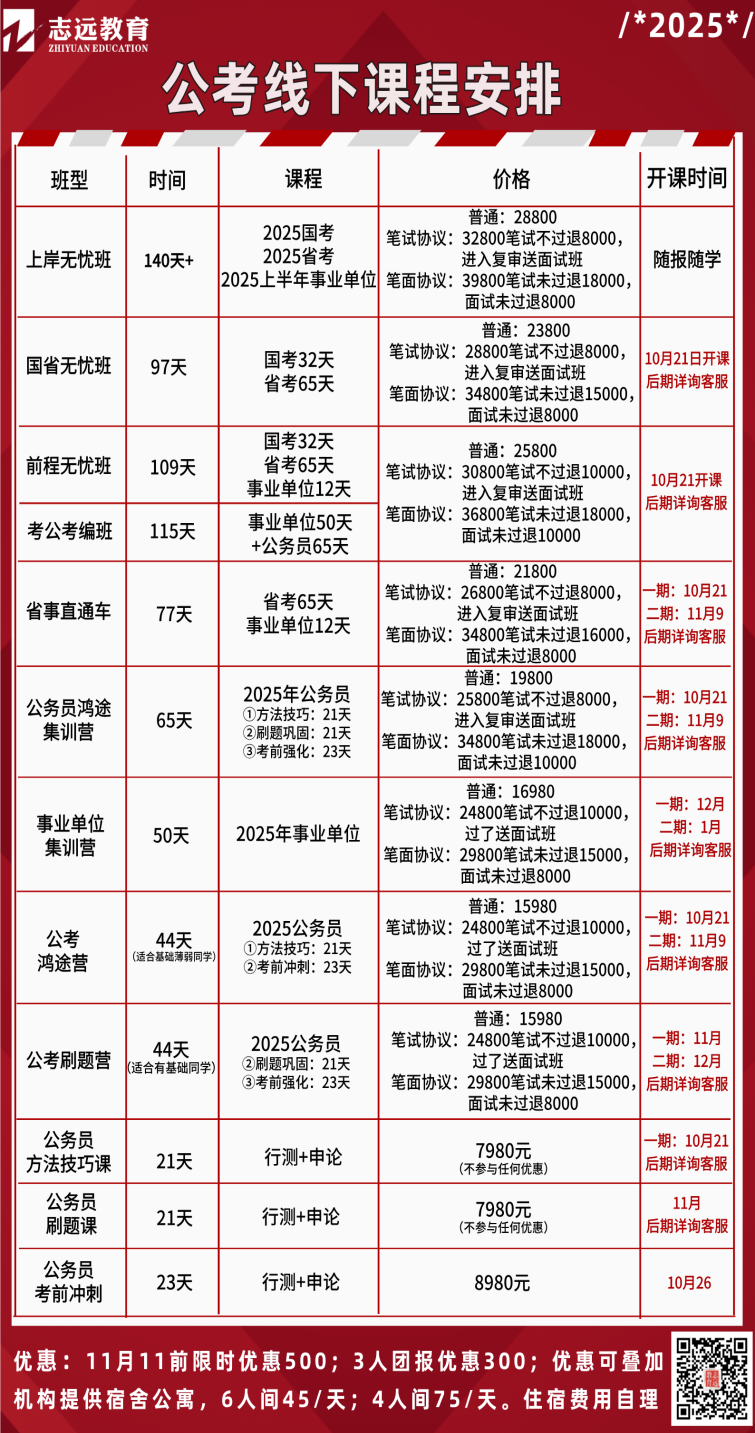


志远教育官网

微信二维码
微信号:17792273747Copyright © 陕西志远鸿途教育科技有限公司 版权所有
备案号:陕ICP备14003123号-1