知识点3:平均数
平均数应用题的基本数量关系如下:
总数量和÷总份数=平均数;
平均数×总份数=总数量和;
总数量和÷平均数=总份数
例题1.一个民警,2004 年一年中,有3个月的月平均收入为1760 元,有4个月的月平均收入为1800元,另有5个月的月平均收入为1824 元,问这个民警2004 年的月平均收入为多少元?
A.1789 B.1798 C.1800 D.1802
【志远快解】:答案C。解析:根据平均数定义可知,这个民警2004 年的月平均收入为
。
例题2.六个自然数的平均数是7,其中前四个的平均数是8,第四个数是11,那么后三个数的平均数是( )。
A.5 B.6 C.7 D.8
【志远快解】:答案C。解析:六个数的和为42,前四个数的和为32,则后两个数的和是10。第四个数为11,因此后三个数的和为21,平均数为7。
例题3.有四个数,去掉最大的数,其余三个数的平均数是41;去掉最小的数,其余三个数的平均数是60;最大数与最小数的和是95。那么这四个数的平均数是多少?( )
A.49.75 B.51.25 C.53.75 D.54.75
【志远快解】:答案A。解析:去掉最大的数,其余三个数的总和为41×3=123;去掉最小的数,其余三个数的总和为60×3=180;又知最大数与最小数的和为95,则123+180+95=398是四个数总和的两倍,所以四个数的平均数为398÷2÷4=49.75,选择A。
1.解题方法
1.1求最大公约数的方法
①分解质因数法:先分解质因数,然后把相同的因数连乘起来。
②短除法:先找出所有共有的约数,然后相乘。
1.2求最小公倍数的方法
①分解质因数法:先把这几个数分解质因数,再把它们一切公有的质因数以及每个数独有的质因数全部连乘起来,所得的积就是它们的最小公倍数。
②短除法:把除得的所有约数连乘起来,即得最小公倍数。
2.相关性质
2.1两个数分别除以它们的最大公约数,所得的商一定互质。
2.2两个自然数的最大公约数与最小公倍数的乘积等于这两个数的乘积。
2.3约数是成对出现的。
2.4平方数的约数是奇数个
知识点4:公倍数和公约数
例题1.有两个两位数,这两个两位数的最大公约数与最小公倍数的和是91,最小公倍数是最大公约数的12倍,求这较大的数是多少?( )
A.42 B.38 C.36 D.28
【志远快解】:答案D。解析:这道例题非常清晰的点明了主旨,就是最大公约数与最小公倍数问题,那么我们可以根据定义来解决。这两个数的最大公约数是91÷(12+1)=7,最小公倍数是7×12=84,故两数应为21和28。
例题2.三根铁丝,长度分别是120厘米、180厘米、300厘米,现在要把它们截成相等的小段,每段都不能有剩余,那么最少可截成多少段?( )
A.8 B.9 C.10 D.11
【志远快解】:答案C。解析:这道例题中隐含了最大公约数的关系。“截成相等的小段”,即为求三数的公约数,“最少可截成多少段”,即为求最大公约数。每小段的长度是120、180、300的约数,也是120、180和300的公约数。120、180和300的最大公约数是60,所以每小段的长度最大是60厘米,一共可截成120÷60+180÷60+300÷60=10段。
例题3.一个小于200的数,除以24或36都有余数16,则这个数是( )。
A.52 B.78 C.88 D.156
【志远快解】:答案C。解析:这道例题中隐含了最小公倍数的关系。“除以24或36都有余数16”,说明此数减去16,即为24和36的公倍数。24和36的最小公倍数为72,则此数应为72+16=88.
例题4.甲、乙、丙、丁四个人去图书馆借书,甲每隔5天去一次,乙每隔11天去一次,丙每隔17天去一次,丁每隔29天去一次。如果5月18日他们四个人在图书馆相遇,问下一次四个人在图书馆相遇是几月几号?( )
A.10月18日 B.10月14日 C.11月18日 D.11月14日
【志远快解】:答案D.解析:甲每隔5天去一次,意思是每6天去一次,依此类推,也就转化为求6,12,18,30的最小公倍数,即180;也就是在5月18的基础上往后180天,再考虑5,7,8,10四个月是大月,可知答案为D。
例题5。有四个自然数A、B、C、D,它们的和不超过400,并且A除以B商是5余5,A除以C商是6余6,A除以D商是7余7。那么,这四个自然数的和是( )。
A.216 B.108 C.314 D.348
【志远快解】:答案C.解析:自然数A是5,6,7的公倍数,5,6,7的最小公倍数是210,而A小于400,所以A=210,B=A/5-1=41,同理得出C=34,D=29,210+41+34+29=314。
知识点5:数列运用
1.等差数列
通项公式:an=a1+(n-1)d=am+(n-m)d
求和公式:
(3)特殊性质:在等差数列{an}中,若m±n=p±q,则am±an=ap±aq
例题1.已知数列1,4,7,10,……,问58 应该是其中的第几项?
A.20B.18 C.19 D.21
【志远快解】:答案A。解析:题中是以1为首项,以3为公差的等差数列。1+(n-1)×3=58,计算可得n=20
A.9 B.10 C.11 D.12
例题2.一辆公共汽车有78个座位,空车发出。第一站上1 位乘客,第二站上2 位乘客,第三站上3位乘客,且中途没有乘客下车,依此类推多少站以后,车上坐满乘客?
【志远快解】:答案D。解析:从第一站开始,每站上车人数分别是从1开始的连续自然数,且已知到第n站后车上的人数之和为78,可直接利用等差数列求和公式
,得到n=12时,即12站以后,车上坐满乘客。
例题3.1992是24 个连续偶数的和,则这24 个连续偶数中最大的一个是( )。
A.84 B.106 C.108 D.130
【志远快解】:答案B。解析:设最大数为x,根据等差数列求和公式可列方程(x+x-23×2)×24÷2=1992,解得x=106。
例题4.一群羊中,每只羊的重量数不相等且均为整数,其总重量为65 公斤。已知:最轻的一只羊重7 公斤,除去一只10 公斤的羊外,其余各只羊的体重恰好组成一等差数列,则这群羊共有几只?
【志远快解】:答案6。解析:由题意a1=7,
;10不属于这个等差数列,说明d 不能取1,3。仅当d=2 时,n有解为5,所以一共有5+1=6只羊。
2.等比数列
通项公式:an=a1qn-1=amqn-m
求和公式:
例题5:已知{an}是等比数列,且an0,a2×a4+2a3×a5+a4×a6=25,那么a3+a5的值是( )。
A.5 B.6 C.7 D.25
【志远快解】:答案A。解析:因为是等比数列,所以a2×a4=a3²,a4×a6=a5²(等比中项的性质)所以,原式化为:a3²+2a3×a5+a5²=25,即:(a3+a5)²=25,因为an0,所以:a3+a5=5。
例题6:甲、乙两个车间生产同一种仪器,甲车间生产的仪器数量每个月保持不变,乙车间生产的仪器数量每个月增加一倍。已知一月份甲、乙两个车间生产的仪器总数是98件,二月份甲、乙两个车 间生产的仪器总数是106 件。那么乙车间生产的仪器数量第一次超过甲车间生产的仪器数量是在( )。
A.3月 B.4月 C.5月 D.7月
【志远快解】:答案C。解析:乙车间一月份产量为106-98=8台,甲车间一月份产量为98-8=90台,且乙车间每个月的产量是首项为8、公比为2的等比数列。设在n月份时,乙车间产量第一次超过甲 车间产量,列不等式组得8×2n-190,8×2n-290,解得n=5。
联系我们:
更多考试信息请关注:陕西志远教育官网(www.zyhtedu.org)
微信公众号:sxzyedu
QQ:623813217
志远教育,让您的起点与众不同!祝各位亲爱的考生圆梦2024!
| 西安校区:西安市雁塔区阳阳国际B座18楼 | 电话:029-87871887 17792273747(同微信) |
| 咸阳校区:咸阳市财富中心 | 电话:029-33275952 18142418653(同微信) |
| 延安校区:延安市东大街7天连锁酒店 | 电话:15353313055(同微信) |
| 渭南校区:渭南师范校内生活区 | 电话:18064315951(同微信) |
| 蒲城校区:迎宾路北段(火锅先生北邻) | 电话:18142418653(同微信) |
| 富平校区:莲湖大街中段(红莲酒店对面) |
电话:18142418353(同微信) |
| 铜川校区:铜川市宜君县南山公园 | 电话:15353313055(同微信) |
课程推荐: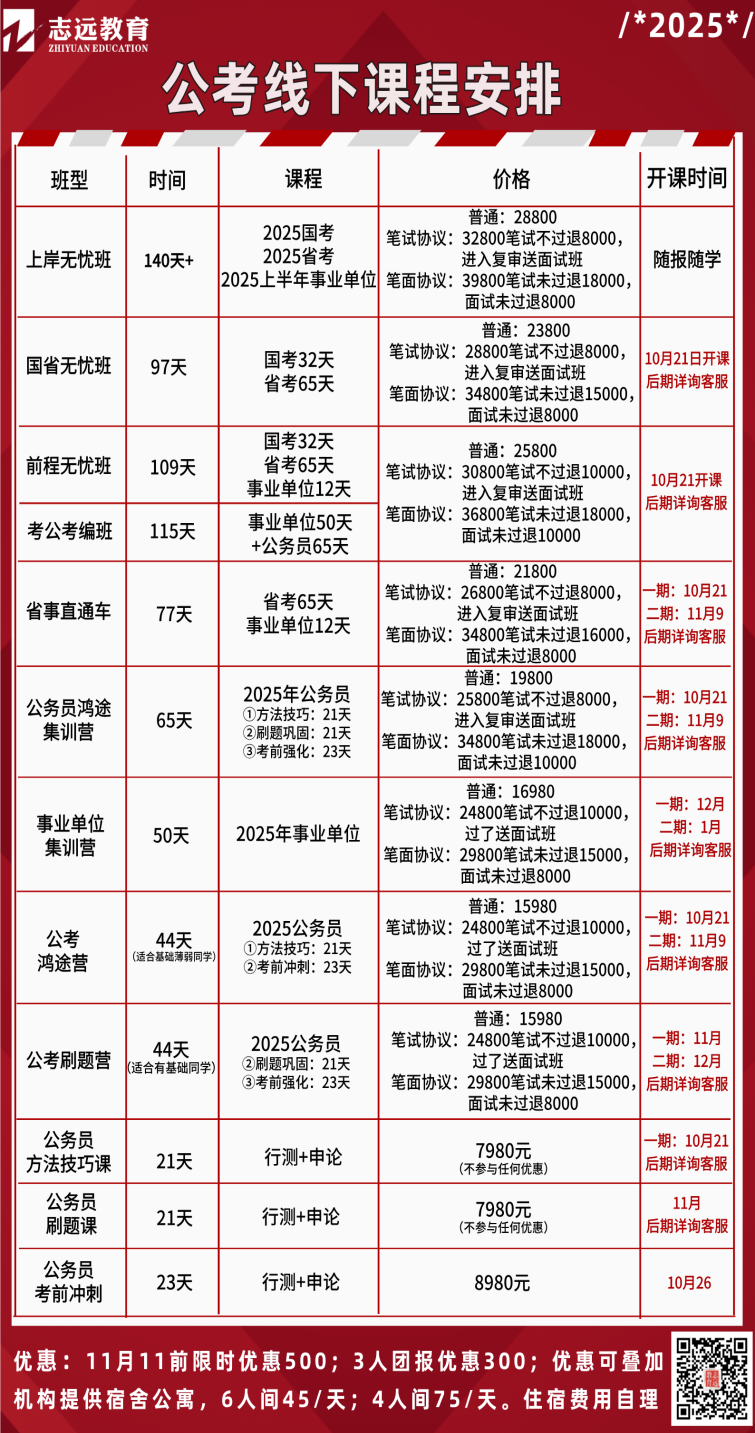


志远教育官网

微信二维码
微信号:17792273747Copyright © 陕西志远鸿途教育科技有限公司 版权所有
备案号:陕ICP备14003123号-1