
知识点6:和定最值
它一般分为三种题型:同向,逆向,混合类,这三种难度是逐层递进的,但解题的核心不变,即:若要使某个量最大,其余量应尽可能小。反之,要使某个量最小,其余量应尽可能大。
1.同向和定最值
1.1问法:“求最大值的最大值”或“求最小值的最小值”
1.2求解方法:列举法
例题1.现有26株树苗,要分植于5片绿地上,若要使每片绿地上分得的树苗数各不相同,则分得树苗最多的绿地最多可以分得几株树苗?
【志远快解】:要求最大量的最大值,并且量各不相同,就应该使其他值尽可能的小,所以最小就应该为1棵,其次为2棵,3棵,4棵,共10棵,所以树苗最多的绿地最多可以分得26-10=16株。
例题2.6个数的和为48,已知各个数各不相同,且最大的数是11分,则最小数最少是多少?
要求最小量的最小值,并且量各不相同,就该使其他值尽可能的大,所以最大为11分,其次为10分,9分,8分,7分,共45分,所以最小数的最少为48-45=3分。
2.逆向和定最值
2.1.问法:“求最大值的最小值”或“求最小值的最大值”
2.2.求解方法:方程法
例题3.某单位2011年招聘了65名毕业生,拟分配到该单位的7个不同部门,每个部门分得的人数不一样,假设行政部门分得的毕业生人数比其他部门都多,问行政部门分得的毕业生人数至少为多少名?
【志远快解】:要求最大量的最小值,就应该使其他值尽可能的大,但不超过最大值。设行政部门分得的毕业生人数最少为X,则与X想接近的值就为x-1,依次x-2……到x-6,把这几个数相加等于65,所以得到方程:x+x-1+x-2+x-3+x-4+x-5+x-6=65,求解得x=12……2,剩余的两个人只能加在第一多的和第二多的两个部门,否则与题意就不符合,所以行政分得的人数至少为12+1=13人。
例题4:现有26株树苗,要分植于5片绿地上,若要使每片绿地上分得的树苗数各不相同,则分得树苗最少的绿地最多可以分得几株树苗?
【志远快解】:要求最小量的最大值,就应该使其他值尽可能的小,但要大于最小值,所以体现的是一个接近的核心,设分得树苗最少的绿地最多可以分得X株树苗,第二小的就应该为X+1,依次X+2……X+4,所以列出方程X+X+1+X+2+X+3+X+4=26,X=3……1,剩余的1棵应该加在第一多的那块地上,如果加在最少的绿地上,则与前一棵的数目就是一样的,与题意不符合,所以,分得最少的绿地最多可以分得3株。
3.混合极值问题:
3.1.问法:“求第N大的数的最大值”或“求第N大的数的最小值”
3.2.求解方法:同时考虑同向极值和逆向极值
例题5.100人参加7项活动,已知每个人只参加一项活动,而且每项活动参加的人数都不一样。那么,参加人数第四多的活动最多有几人参加?
【志远快解】:求第四多的活动最多有几人参加。以第四多为分界点,分界点之前是求最大量的最大值,所以属于同向和定最值,用列举法,最少的为1,依次为2,3,4;再从分界点之后来看,是求最小量的最大值,属于逆向和定最值,用列方程的方法求解,设第四多的为x,依次就为x+1,x+2,x+3,列等式x+x+1+x+2+x+3=100-(1+2+3),x=22。所以第四多的活动最多有22人。
例题.现有26株树苗,要分植于5片绿地上,若要使每片绿地上分得的树苗数各不相同,则分得树苗第二多的绿地最少可以分得几株树苗?
【志远快解】:求第二多的绿地最少分得几株树苗,以第二多为分界点,分界点之后是求最大量的最大值,所以属于同向和定最值,用列举法,最少的为1,依次为2,3;再从分界点往前看,是求最小量的最大值,属于逆向和定最值,用列方程的方法求解,设第二多的为x,第一多就为x+1,列方程x+x+1=26-(1+2+3),x=9……1,剩余的1棵只能加在最多的那片绿地上,所以第二多的绿地最少可以分到9株。
知识点7:同余定理
同余在考试的时候也会经常性的出现,它一般都是与整除思想相结合的,在备考的过程中要分清楚同余的几种情况,同余特性经常会与中国剩余定理混淆,所以在备考时要抓住两者的区别点,避免考试时出错。
1.同余概念
两个整数a和b,除以一个大于1的自然数m所得余数相同,就称a和b对于m同余。
例:21÷4余1,17÷4余1,所以17和21对于4同余。
2.同余特性
(1)余数的和决定和的余数
例:23、16除以5的余数分别是3和1,所以23+16=39除以5的余数等于4,即两个余数的和3+1。
(2)余数的差决定差的余数
例:23,16除以5的余数分别是3和1,所以 23-16=7除以5的余数等于2,即两个余数的差3-1。
(3)余数的积决定积的余数
例:23,16除以5的余数分别是3和1,所以23×16除以5的余数等于3×1=3。
(4)余数的幂决定幂的余数。
例1.求20122012÷5的余数。
一个2012除以5余2,根据余数的积决定积得余数,所以20122012÷5的余数和22012÷5的余数是一样的,又因为22012=16503,所以16÷5余1,所以20122012÷5的余数和1503÷5的余数一样,都为1。
例题1.已知a除以2余1,那么27a+20032除以2余几?( )
A.1 B.2 C.3 D.4
【志远快解】:答案A.27是2的倍数,所以27a是2的倍数,20032除以2余1,则27a+20032除以2余0+1=1。答案选择A。
例2.今天是星期六,请问再过2010天是星期几?再过20102010天是星期几?再过20122012天是星期几?( )
【志远快解】:2010除以7余1,故再过2010天是星期日。又根据余数的幂决定幂的余数,所以20102010除以7的余数与12010除以7的余数相同,因此20102010除以7的余数为1,所求为星期日。同理,根据余数的幂决定幂的余数,2012除以7余3,所以20122012除以7的余数与32012除以7的的余数相同,又因为3的平方为9,9除以7余数为2,32012=91006,所以最终的余数取决于21006 =8335 ×2=1335×2=2,即为2,所以所求为星期一。
例题3。商店里有6箱货物,分别重15、16、18、19、20、31千克,两个顾客买走了其中五箱。已知一个顾客买的货物重量是另一个顾客的2倍,商店剩下的一箱货物重( )千克?( )
A. 16 B. 18 C. 19 D. 20
【志远快解】:答案D。和的余数等于余数的和。
采用这种方法的解题点也是:“一个顾客买的货物重量是另一个顾客的2倍”。
首先:也是将6箱货物相加:15+16+18+19+20+31=119;
加后的结果除以3,即119÷3=39…2;此时和的余数等于2。
然后在15、16、18、19、20、31六个数中找除以3余2的数,这个数就是剩下来的没拿走的那个。
15÷3=5…0; 16÷3=5…1
18÷3=6…0; 19÷3=6…1
20÷3=6…2; 31÷3=10…1
这时将所有与数相加得:0+1+0+1+2+1=5;
5÷3=1…2;
运用和的余数等于余数的和,所以找到除以3余2的数,就是剩下来的那箱货物,即货物20千克是被剩下来的。因此,本题选D。
[随堂练习一]
1.两个派出所某月内共受理案件160起,其中甲派出所受理的案件中有17%是刑事案件,乙派出所受理的案件中有20%是刑事案件,问乙派出所在这个月中共受理多少起非刑事案件?( )
A.48 B.60 C.72 D.96
2.某个月有五个星期六,已知这五个日期的和为85,则这个月中最后一个星期六是多少号?( )
A.10 B.17 C.24 D.31
3.张老师给幼儿园两个班的孩子分水果,大班每人分得5个橘子和2个苹果,小班每人分得3个橘子和2个苹果。张老师一共分发了135 个橘子和70个苹果,那么小班共有多少个孩子?( )
A.20 B.15 C.18 D.12
4.农业站有一批化肥,第一天卖出一半又多15吨,第二天卖出余下的一半多8吨,第三天卖出180 吨,正好卖完,这批化肥原来有( )吨。
5.有一个电子钟,每到整点响一次铃,每走9分钟亮一次灯。中午12点整时,电子钟既响铃又亮灯。求下一次既响铃又亮灯是下午几点钟?( )
A.2 B.3 C.5 D.7
6.某单位购进92箱桔子,每箱至少110个,至多138个,现将桔子数相同的作为一组,箱子数最多的一组至少有几箱?( )
A.3 B.4 C.5 D.6
联系我们:
更多考试信息请关注:陕西志远教育官网(www.zyhtedu.org)
微信公众号:sxzyedu
QQ:623813217
志远教育,让您的起点与众不同!祝各位亲爱的考生圆梦2024!
| 西安校区:西安市雁塔区阳阳国际B座18楼 | 电话:029-87871887 17792273747(同微信) |
| 咸阳校区:咸阳市财富中心 | 电话:029-33275952 18142418653(同微信) |
| 延安校区:延安市东大街7天连锁酒店 | 电话:15353313055(同微信) |
| 渭南校区:渭南师范校内生活区 | 电话:18064315951(同微信) |
| 蒲城校区:迎宾路北段(火锅先生北邻) | 电话:18142418653(同微信) |
| 富平校区:莲湖大街中段(红莲酒店对面) |
电话:18142418353(同微信) |
| 铜川校区:铜川市宜君县南山公园 | 电话:15353313055(同微信) |
课程推荐: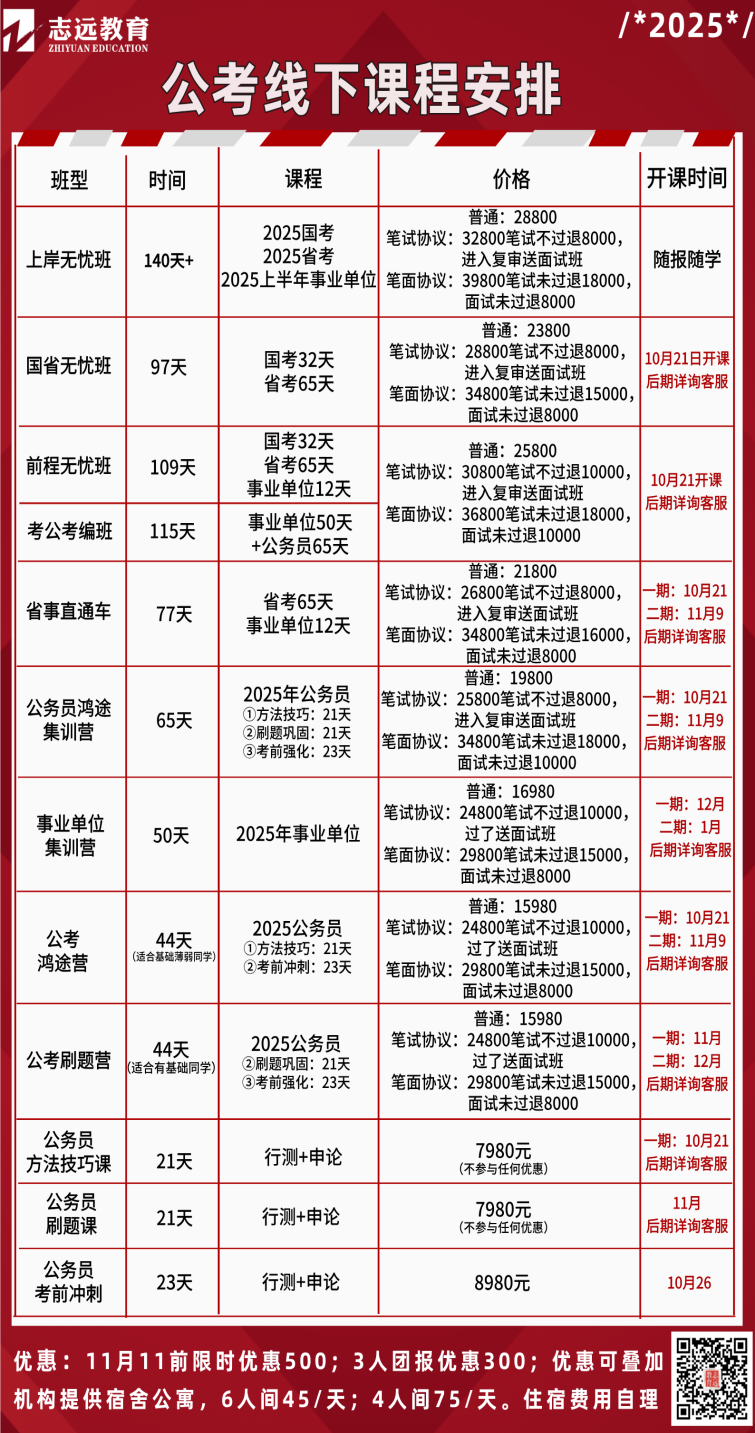


志远教育官网

微信二维码
微信号:17792273747Copyright © 陕西志远鸿途教育科技有限公司 版权所有
备案号:陕ICP备14003123号-1